Uji hipotesis 2 rata-rata

Assalamualaikum teman-teman, dibawah ini saya membagikan ppt dari tugas mata kuliah statistika dasar materi Uji hipotesis 2 rata-rata. dalam ppt ini kami memberikan beberapa grafik untuk mempermudah kalian belajar materi ini . semoga bermanfaat yaa

Uji hipotesis 2 rata rata from Sriut_16

Read More

Distribusi Binomial dan Poisson

Assalamualaikum teman-teman, disini saya akan memabagikan ppt. ini adalah materi distribusi binomial dan poisson pada mata kuliah statistika dasar. Bagi teman-teman yang ingin belajar materi ini semoga yang saya bagikan ini bisa membantu kalian memahaminya okee!!

Distribusi binomial dan poisson from Sriut_16

Read More

CABRI 3D

Cabri 3D mampu menyajikan objek geometri yang sangat baik dan dapat dilihat dari berbagai sudut pandang serta mampu menentukan hubungan antara objek-objek tersebut. Kegunaan lain dari program 3D Cabri adalah menghasilkan ekspresi aljabar dari bentuk-bentuk yang diciptakan, perhitungan parameter seperti panjang, luas, diameter, dan sebagainya.Ini adalah program yang sangat tepat bagi guru dan siswa yg belajar matematika.
Bagi kalian yang ingin punya aplikasi ini silahkan  KLIK DISINI

Read More

JURNAL PENDIDIKAN MATEMATIKA

Assalamualaikum teman-teman yang lagi butuh jurnal-jurnal pendidikan matematika sebagai referensi penelitian, disini saya akan membagikan link-link yang dapat membantu kalian mendapatkannya. saya mendapatkan daftar link ini dari blog sholihatunnisa96.blogspot.com  teman saya yang baik hati mau berbagi sumber jurnal pendidikan matematika yang teman-teman cari. Semoga bermanfaat yaa

Read More

MAKALAH PENGELOLAAN PENDIDIKAN

Pengelolaan Peserta Didik

OLEH:

KELOMPOK 4

ASTI ARIANI                                 (06081381419049)

SUCI AGUSTINA                          (06081381419051)

SRI UTAMI                                     (06081381419058)

Dosen Pembimbing:

1.    Dr. Nyimas Aisyah, M.Pd

2.    Meryansumayeka, S.Pd,. M.Sc

FAKULTAS KEGURUAN DAN ILMU PENDIDIKAN

PENDIDIKAN MATEMATIKA

2016

Read More

Soal Kekongruenan Interaktif

Teman-teman yang ingin menguji kemampuan memahami konsep kekongruenan, saya akan membagikan beberapa soal yang dapat membuat kalian tidak bosan mengerjakannya. Dalam soal-soal ini kalian bisa membuktikan apakah 2 bangun itu kongruen atau tidak dengan cara tranformasi (mentranslasikan, rotasi, dan merefleksikan) secara otomatis. Kalian penasaran dengan soal nya, untuk mencoba silahkan KLIK DISINI 
  

Selain itu disini juga saya akan membagikan soal-soal yang seru dan juga menantang. Hayo siapa yang berani mencoba silahkan KLIK DISINI

SELAMAT MENCOBA.........

Read More

Video Memahami Konsep Kekongruenan

Teman-teman kali ini saya akan berbagi video tentang kekngruenan. Dengan melihat video ini kalian akan lebih memahami konsep kekongruenan itu sendiri. Video ini dibuat oleh MashUp Math. 

Semangat ya belajarnya jangan mudah menyerah oke!!

Read More

PUZZLE TELUR

MENETASKAN TELUR (Hatching the Egg)

               Kegiatan menetaskan telur dari Puzzle telur ini menantang siswa untuk mengatur ulang sepuluh  potongan telur kertas untuk menghasilkan sejumlah bentuk yang berbeda menyerupai burung. Melakukan hal ini akan melatih kemampuan visualisasi siswa.

               Teka-teki ini adalah bagian dari puzzle yang menantang, banyak solusi. Tidak seperti puzzle tangram, dan sebagian besar dari teka-teki lainnya, Penetasan Telur memiliki potongan yang bulat serta tepi lurus. Sama seperti teka-teki lainnya, namun potongan dapat ditempatkan bersama-sama dalam sejumlah cara yang berbeda untuk membuat menarik, dan dikenali bentuknya.  Dalam kasus Penetasan Telur, lebih dari 50 bentuk menyerupai burung dapat dibuat. Karena teka-teki ini memiliki begitu banyak kemungkinan solusi, dapat digunakan selama jangka waktu.

               Kegiatan ini siswa diberikan dua kertas.Lembar pertama adalah Puzzle yang berbentuk telur. Lembar kedua berisi enam burung yang dapat dibuat. Dalam proses bermain dengan teka-teki, siswa juga dapat menemukan bentuk burung lain yang tidak digambarkan. Ketika ini terjadi, mereka harus didorong untuk membuat catatan dari kreasi mereka.
 

 Berikut lembar yang harus diberikan kepada siswa:  

Petunjuk : Gunting puzzle diatas menjadi sepuluh bagian setelah itu susun menjadi burung-burung seperti gambar di bawah ini

Sumber : http://blog.aimsedu.org/2014/04/15/hatching-the-egg/

Read More

Mengingat Bentuk dan Sifat Bangun Datar

Mengingat Bentuk dan Sifat Bangun Datar

Teman-teman masih ingatkah kalian bangun-bangun datar yang ada dikehiduan sehari-hari?


Bangun-bangun datar ini sangat perlu kita pahami dan kuasai karena untuk belajar geometri pada matematika seperti kekongruenan dan kesebangunan, bangun ruang dan masih banyak lagi materi-materi yang lain yang memerlukan pemahaman tentang bangun-bangun datar.

Berikut beberapa bangun datar yang wajib dikuasai siswa beserta sifat-sifatnya :

Gambar dan Nama Bangun	Deskripsi
Persegi	Keempat sisinya sama panjang (AB=BC=CD=DA).Keempat sudutnya sama besar.
Persegi panjang	Ada2 pasang sisi yang panjangnya sama (AB=CD, BC=DA).Keempat sudutnya juga sama besar.
Jajar Genjang	Sisi sejajar sama panjang (AB=CD, BC=DA.Sudut yang berhadapan sama besar.
Trapesium	Dua sisi tidak sejajar panjangnya sama (AD=BC).Dua sisi sejajar panjangnya tidak sama (AB//CD). Sudut yang bersisian sama besar.
Belah Ketupat	Keempat sisinya sama panjang (AB=BC=CD=DA).Sudut yang berhadapan sama besar). Diagonal berpotongan saling tegak lurus.
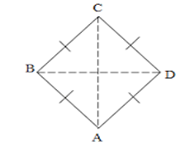
Layang-Layang	Ada2 pasang sisi sama panjang (AB = AD, BC=CD).Sudut yang berhadapan sama besar. Diagonal saling tegak lurus.
Segitiga	Segitiga terdiri dari tiga sisi yang berupa garis lurus dan tiga sudut. Jumah ketiga sudut segitiga adalah 1800

NOTE

 Tahukah kalian bahwa persegi adalah sebuah persegi panjang yang istimewa, karena persegi memiliki sisi-sisi yang sama panjang.


Sumber :
 https://pintarmatematika.wordpress.com

Read More

Mengenal THALES penemu konsep kesebangunan

 Thales adalah seorang filsuf yunani yang hidup pada abad ke-6 SM. Lahir di kota Miletus. Awalnya Thales adalah seorang pedangang, profesi yang membuatnya sering melakukan perjalanan. Kondisi kota Miletos yang cukup makmur memungkinkan orang-orang di sana untuk mengisi waktu dengan berdiskusi dan berpikir tentang segala sesuatu yang ada disekitar mereka, sehingga banyak para filsuf yunani pertama lahir di tempat ini. Pemikiran Thales dianggap sebagai kegiatan berfilsafat pertama karena ia mencoba menjelaskan dunia dan gejala-gejala didalamnya dengan menggunakan rasio manusia dan tidak bergantung pada mitos yang berkembang dimasyarakat. Ia juga dikenal sebagai salah seorang dari Tujuh Orang Bijaksana (dalam bahasa Yunani hoi hepta sophoi), yang oleh Aristoteles diberi gelar 'filsuf yang pertama'. Selain sebagai filsuf, Thales juga dikenal sebagai ahli geometri, astronomi, dan politik. Pada bidang matematika, Thales mengungkapkan salah satu gagasan yang cukup fenomenal, yakni dibidang kesebangunan. Diceritakan bahwa dia dapat menghitung tinggi piramida dengan menggunakan bantuan dari bayangan suatu tongkat. Thales menggunakan kenyataan bahwa segitiga yang dibentuk oleh piramida dan bayangannya sebangun dengan segitiga kecil yang dibentuk oleh tongkat dan bayangannya. Dengan menggunakan perbandingan kesebangunan dua segitiga itu ia dapat memperkirankan tinggi dari piramida tersebut. Selain itu Thales juga mampu mengukur jauhnya kapal di laut dari pantai. Kemudian Thales menjadi terkenal setelah dia berhasil memprediksi terjadinya gerhana matahari pada tanggal 28 Mei atau 30 September tahun 609 SM. Dia dapat melakukan prediksi tersebut karena dia telah mempelajari catatan-catatan astronomis yang tersimpan di Babilonia sejak tahun 747 SM. Thales tidak meninggalkan cukup bukti tertulis mengenai pemikiran filsafatnya. Thales juga dianggap sebagai perintis filsafat alam (natural philosophy). Sumber : http://www.konsep-matematika.com https://id.wikipedia.org/wiki/Thales

Read More